| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 딥러닝
- 백준 5525번
- React Native
- 머신러닝
- 문자열
- 스터디
- 데베
- 네트워크
- 깃허브 토큰 인증
- 모두의네트워크
- 리액트 네이티브 시작하기
- 모두를위한딥러닝
- 정리
- 리액트 네이티브 프로젝트 생성
- 백준
- 모두의 네트워크
- 자바
- 깃허브 로그인
- SQL
- 백준 4358번
- 깃 터미널 연동
- 지네릭스
- 백준 4949번
- 모두를 위한 딥러닝
- 깃 연동
- 팀플회고
- 데이터베이스
- 리액트 네이티브
- 백준 4358 자바
- HTTP
- Today
- Total
솜이의 데브로그
스터디 ) 모두를 위한 딥러닝 lec 4~6 정리 본문
<Lec 4 정리>
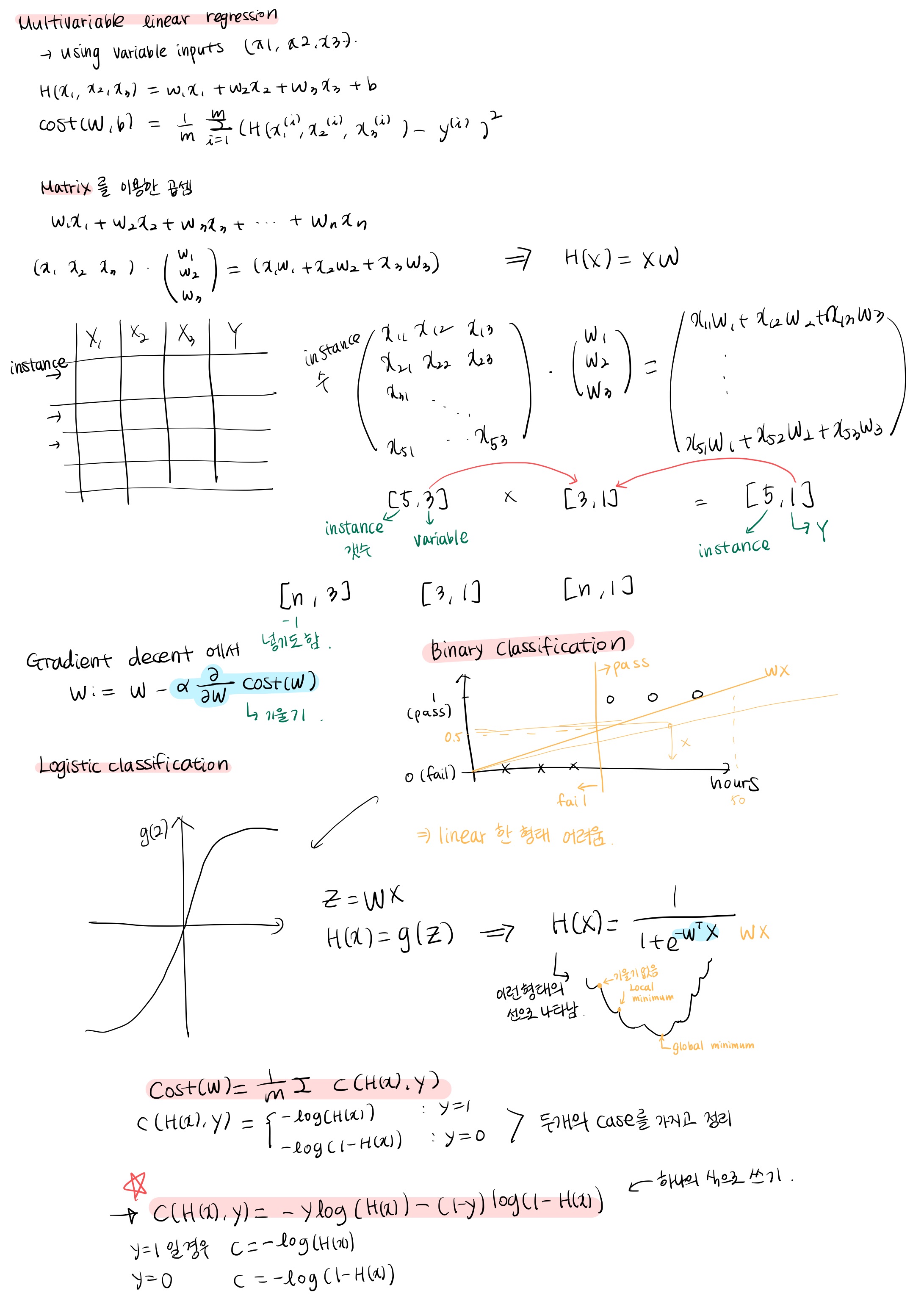
Multivariable linear regression (여러개의 변수 사용)
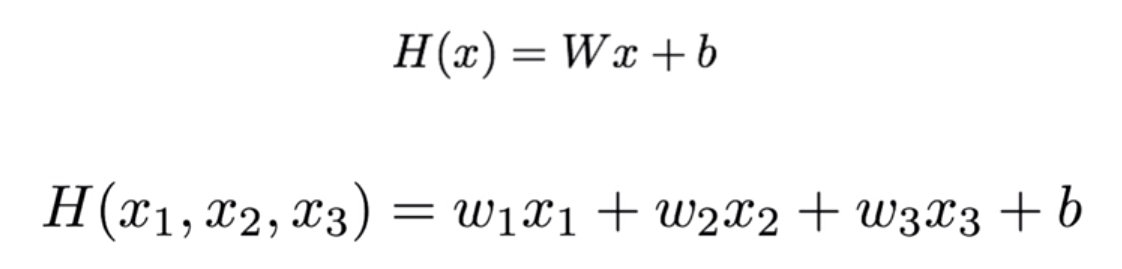
식을 다음과 같이 바꿔서 사용. 위의 예시는 input이 3개인 경우 hypothesis 식
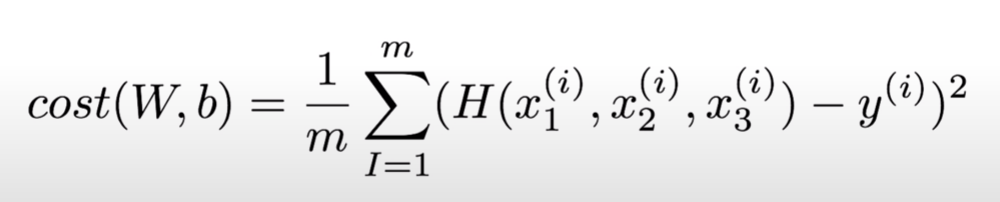
같은 경우 Cost Function의 식은 이렇게 바꿀 수 있다.
variable이 많아 질 경우 식이 너무 복잡해지므로 Matrix 의 곱셈을 이용한다.
-> H(X) = XW
각 변수에 대한 인스턴스가 여러개 있어도 matrix를 사용하면 곱셈에 문제가 없다.
H(X)의 행 = instance 개수
H(X)의 열 = Y 값 개수
두가지 값이 주어졌을 때 W의 크기 결정
W의 행 = H의 열
W의 열 = H(X)의 열
출력값 Y가 1개 이상인 경우
matrix의 곱셈 결과 값의 열이 1개 이상.
TensorFlow에서 사용하는 경우 H(X) = XW 순으로 써주는 것이 matrix 계산 구현이 가능하므로 최대한 이 표기법으로 사용하기
<Lec 5 정리>
Logistic classification
- 정확도가 높은 알고리즘
Binary classification
- 정해진 두개의 카테고리 중 하나를 선택. (ex : Spam main Detection)
- 0/1 로 encoding 하여 표현한다.
- 따라서 Linear 한 그래프 형태로 표현하기 어렵다.
Linear 한 형태와 비슷하게 표현하기 위해 0과 1로만 결과가 나오도록 압축하는 식 사용.
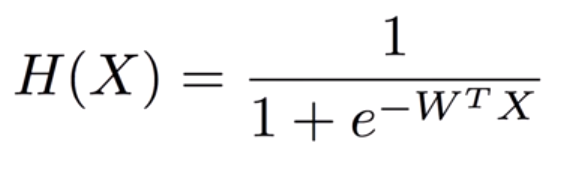
위와 같은 가설을 세워 사용한다. 값은 0에서 1사이로 나오게 된다.
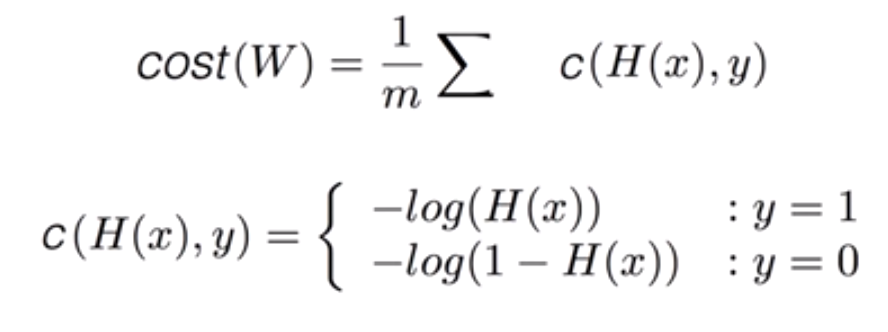
Cost Function은 위와 같다.
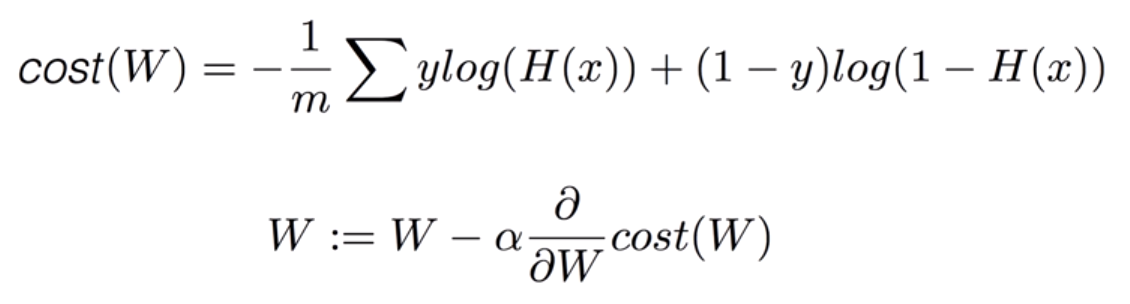
위의 식은 Cost Function 을 조건을 나누지 않고 하나의 식으로 만든 것이다. (Tensorflow에서 사용하기 편리하도록)
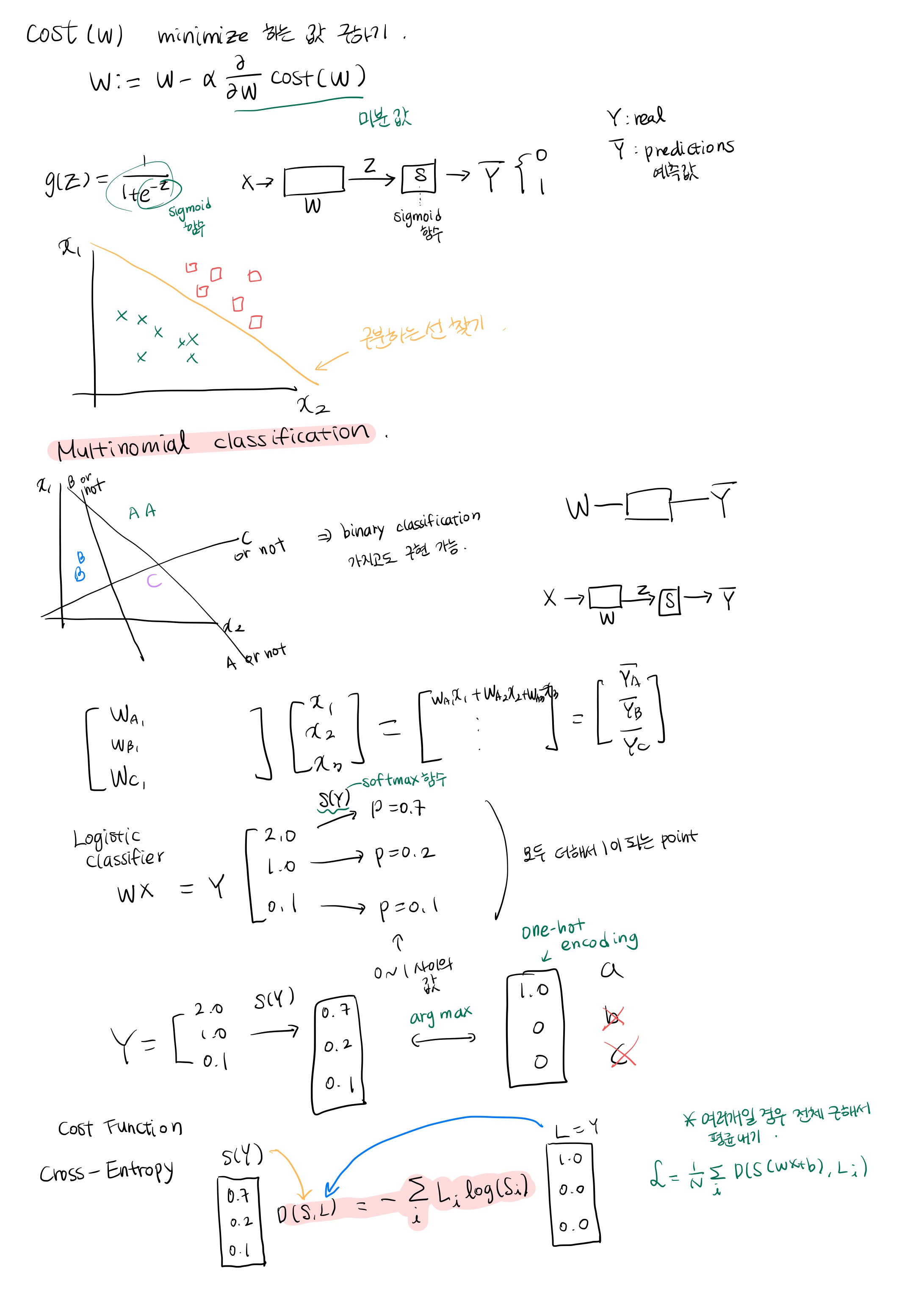
밑의 식은 W값 변화시키며 Cost를 최소화하는 값 구하기.
<Lec 6 정리>
Multinomial Classification
- 여러개로 분류하는 경우 분류할 수 있는 선 찾기.
- Binary classification 으로 각각의 값 분류 가능. ex) A or not 선 / B or not 선 ...
각각의 결과 값에 sigmoid 함수 적용
SoftMax
- Logistic classifier를 통해 WX = Y 값을 내면, sigmoid 함수에 적용해 값이 0과 1사이의 값으로 나오도록 함.
결과 값의 합은 1이 되어야 함.- 나온 결과 값 중 큰 값을 1로 하고 나머지 작은 값은 무시해도 되는 경우 0 으로 설정. "One-hot encoding"
Cross-entropy : 불확실성의 정도Cross-entropy를 이용하여 cost function 만든다.
S(y): 출력을 softmax로 변환 (예측한 y 값)
L : 실제 값
Logistic cost 와 cross entropy 사실상 같다.
최소화 구하는 법은 Gradient descent를 사용한다. (경사면 타고 내려가 최저값 구하는 알고리즘)
필기 정리
'Machine Learning' 카테고리의 다른 글
| 실습 ) Kaggle house price 실습 (0) | 2021.04.05 |
|---|---|
| 실습 ) Titanic 실습 (0) | 2021.03.29 |
| 스터디 ) 모두를 위한 딥러닝 lec10~12 정리 (0) | 2021.03.22 |
| 스터디 ) 모두를 위한 딥러닝 lec 7~9 정리 (0) | 2021.03.22 |
| 스터디 ) 모두를 위한 딥러닝 lec 1~3 정리 (0) | 2021.03.15 |




